Redes Neuronales III

Entrenamiento por Propagación hacia Atrás

(aprendizaje Supervisado)

El algoritmo de backpropagation se introdujo originalmente en la década de 1970, pero su importancia no se apreció completamente hasta un famoso artículo de 1986 de David Rumelhart, Geoffrey Hinton y Ronald Williams. Este documento describe varias redes neuronales en las que la retropropagación funciona mucho más rápido que los enfoques de aprendizaje anteriores, lo que hace posible utilizar redes neuronales para resolver problemas que anteriormente habían sido insolubles.

Pero, y cómo funciona... En redes neuronales se busca ajustar los pesos de cada neurona de tal manera que se minimice el error. El algoritmo de backpropagation nos indica cuanto de culpa tiene cada neurona del error global cometido.

La forma en que como se calcula la culpa que tiene cada neurona en el error es lo que da sentido al nombre de backpropagation, ya que primeramente calcula la culpa del error de cada neurona de la última capa y lo va propagando hacia atrás para ver cuanta culta tienen el resto.

Se podría decir que pondera el reparto del error para cada una de las neuronas de la red.

El algoritmo de backpropagation determina la culpa del error, calculando las derivadas parciales de la función de coste con respecto a cada una de las variables.

Observa esta imagen a continuación y ve como se van desarrollando los cálculos hacia delante y al llegar al final se regresa por el camino hasta llegar al inicio se modifican los pesos y se vuelve a dirigir hacia delante.

Recuerda este ejercicio 👇es el  ejemplo que vimos en clases y que volví a subir aquí 

en este ejercicio solo fuimos hacia delante. En el algoritmo de Propagación hacia Atrás regresamos y ajustamos pesos de acuerdo a los errores que se hayan encontrado, y volvemos adelante con los ajustes hechos, para encontrar el resultado esperado.

Tarea: las 4 ecuaciones de backpropagation 

REDES NEURONALES II

Redes neuronales no supervisadas

Mapas auto organizativos de Kohonen o self-organizing maps  (SOM)

Conocen los conceptos de algoritmos no supervisados y supervisados por ello, pero como seguramente ya lo olvidaron veamos que son de forma rápida:

Los algoritmos de clasificación no supervisados son aquellos que no requieren etiquetado de cada uno de los vectores de entrada; se suelen llamar también algoritmos auto-asociativos, porque asocian entradas a ellas mismas.

Y bueno comencemos con las redes no supervisadas, y más concretamente sobre los mapas auto organizativos de Kohonen o self-organizing maps  (SOM), que son un algoritmo de redes neuronales no supervisadas que suele ser de los más utilizados - ojo que no es el único-.

Este tipo de redes fue desarrollado por el profesor Teuvo Kohonen (1982) e intenta imitar el comportamiento del cerebro en el tratamiento de la información en ciertos casos concretos. Y es que el cerebro se organiza, corrige errores y procesa nueva información sin tener referencias previas donde apoyarse. Es capaz de crear mapas mentales clasificando la información en determinadas zonas en base a los estímulos  que le llegan. Información con los mismos patrones de entrada o estímulos similares son clasificados en zonas próximas del cerebro.  

También entran dentro de las redes competitivas, porque también imitan la competición de las neuronas cerebrales cuando nueva información es procesada. Solamente las neuronas que más se parecen o están especializadas en un patrón de entrada son activadas y por lo tanto pueden ser consideras como ganadoras recopilando la nueva información. Un esquema habitual de SOM es el siguiente:

Pero bueno es difícil entenderlo de esta manera por ello ve el siguiente video para que podamos entender mejor el concepto de esta red neuronal SOM.

Clasificación de animales

Supongamos ahora que tenemos la siguiente tabla de información acerca de las propiedades de un conjunto de animales:

	Paloma	Gallina	Pato	Ganso	Buho	Halcón	Águila	Zorro	Perro	Lobo	Gato	Tigre	León	Caballo	Cebra	Vaca
Pequeño	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	No	Sí	No	No	No	No	No
Medio	No	No	No	No	No	No	Sí	Sí	Sí	Sí	No	No	No	No	No	No
Grande	No	No	No	No	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí	Sí
2 patas	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	No	No	No	No	No	No
4 patas	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí
Pelo	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí
Pezuñas	No	No	No	No	No	No	No	No	No	No	No	No	No	Sí	Sí	Sí
Melena	No	No	No	No	No	No	No	No	No	Sí	No	No	Sí	Sí	Sí	No
Plumas	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	No	No	No	No	No	No
Caza	No	No	No	No	Sí	Sí	Sí	Sí	No	Sí	Sí	Sí	Sí	No	No	No
Corre	No	No	No	No	No	No	No	No	Sí	Sí	No	Sí	Sí	Sí	Sí	No
Vuela	Sí	No	No	Sí	Sí	Sí	Sí	No	No	No	No	No	No	No	No	No
Nada	No	No	Sí	Sí	No	No	No	No	No	No	No	No	No	No	No	No

Usando las columnas anteriores como vectores de entrenamiento, y un tamaño adecuado del mundo para que los vectores puedan distribuirse en él con comodidad (pero no tan grande como para que no se les olbigue a reorganizarse localmente), podemos obtener una clasificación 2D de los elementos a los que caracterizan (animales), dando relaciones de similaridad (clasificándose) automáticamente:

Aquí hay algo importante y es que los datos se normalizan las componentes de los vectores (ya están normalizados, convirtiendo No = 0, Sí = 1) y se generan pesos al azar con componentes aleatorias entre 0 y 1. En este caso, debido a que cada vector tiene 13 componentes, usamos sólo las 3 primeras para dar una ligera clasificación por colores, pero no reflejan la información adicional que hay en los pesos reales que se usan en el algoritmo.

Puede observarse que la clasificación tiene sentido, ya que agrupa de forma coherente animales que consideramos similares por causas diversas.

¿Y qué aplicaciones tienen este tipo de redes? Han sido ampliamente empleadas, dada la gran capacidad de sintetizar la información de manera muy visual. Además, se preservan las distancias entre los datos de entrada, de tal forma que distancias entre neuronas en el mapa también son distancias equivalentes en los datos de entrada. Han sido ampliamente utilizados para clasificar países en base a su pobreza, clasificar textos y páginas web, música, detección de linfomas en imágenes, procesamiento del lenguaje…

En el ámbito de finanzas han sido empleadas para clasificar acciones y bonos en función de rentabilidad y volatilidad, lo que es útil para gestión de carteras de valores, también para la selección de fondos de inversión, detección de grupos de empresas en problemas financieros y quiebras o  predicción de ratings de las agencias de calificación crediticia entre otros.

La reducción de dimensiones de gran cantidad de información a solamente un mapa bi-dimensional permite procesar y comprender patrones en los datos que de otra forma sería más complicado. Con este artículo se ha pretendido introducir al lector en esta metodología así como el posible interés en alguna de sus versiones (supervised self-organising maps, fuzzy self-organizing maps…).

Tarea: Qué es la normalización de datos, ejemplos de normalizacion de datos- La tarea debe ser enviada a mi correo escaneada o fotografia, pues deben elaborarla a mano. 

Redes Neuronales

Redes neuronales aprendizaje Supervisado y no supervisado

Recordemos un poco de lo que se hablo en las clases presenciales sobre las redes neuronales, recuerda que dijimos: Las redes neuronales artificiales están basadas en el funcionamiento de las redes de neuronas biológicas. Las neuronas que todos tenemos en nuestro cerebro están compuestas de dendritas, el soma y el axón: Las dendritas se encargan de captar los impulsos nerviosos que emiten otras neuronas. Estos impulsos, se procesan en el soma y se transmiten a través del axón que emite un impulso nervioso hacia las neuronas contiguas. 

Para hacer mas sencillo el concepto, diríamos que una red neuronal no es más que una formula matemática que nos permite resolver un problema. 

A esto se le llama perceptron simple ☝

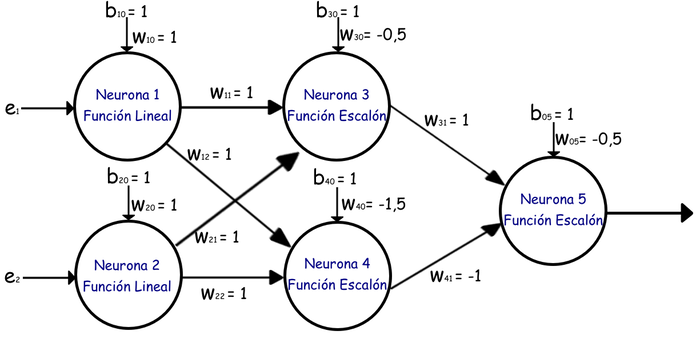
También los hay perceptrones multicapa es decir cuentan con más funciones o formulas que combinadas nos permiten obtener el resultado deseado.

Aquí un ejemplo de un perceptron multicapa👆

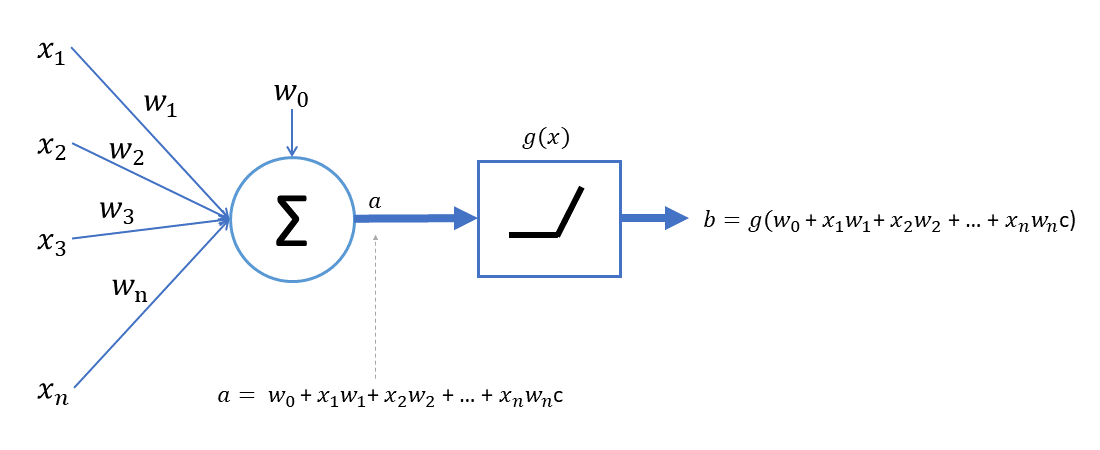
Una red neuronal o perceptron también llamado esta dividido de la siguiente forma, observa la imagen a continuación.

Bueno ahora veamos unos ejemplos que vimos en clase del uso de un perceptron simple y despues un perceptron multicapa.

De forma gráfica tenemos un perceptron que tiene los siguientes datos:

Los datos de entrada serian 3,4 y -2, tiene cada uno de ellos un peso que serian .2,.6 y .01 también llamados ponderación(cual dato tiene más valor o peso respecto a los otros), contamos con una sumatoria y una función de activación.

Para resolver este problema haríamos lo siguiente:

1. Una vez tenemos estos datos y pesos, se deben multiplicar los los datos por sus pesos, y sumar los resultados.

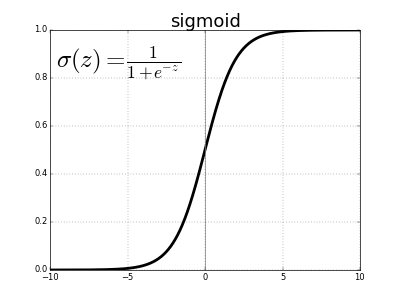
2. el siguiente paso seria llamar a la función de activación. Se han propuesto muchas funciones de activación, pero por ahora describiremos solamente una. Históricamente, la función sigmoide es la función de activación más antigua y popular. Se define como:

Bueno para nuestro caso quedaría así 👇(la e=2.71828  euler aquí 👉 más información si deseas)

Listo tenemos finalizado el ejercicio.

Ahora veamos un perceptron multicapa...

Observemos este ejercicio☝ vean que tenemos los mismos componentes (datos y pesos)  y uno extra el de color violeta llamado umbral sus valores son de 1. Para resolver esta red haríamos lo siguiente:

1. Colocarnos en el primer nodo de la red y ver cuales son sus entradas de datos y pesos

estamos en ese nodo de color azul  de arriba👇 

si nos paramos sobre el vemos que esta recibiendo dos entradas

el 3 y el 1 como pesos y el 1 y 2 como datos, y un umbral de 1

hacemos el calculo 

El resultado es 6, esto mismo haríamos con el otro nodo de abajo, el cual recibe 2 y 4 como pesos, 2 y 1 como datos. hacemos la operación v= (2)*(1) + (2)*(4) + 1=11, recuerda que el 1 del final es el umbral. 

Ahora que ya tenemos los resultados llamamos a la función de activación que para este caso utilizaremos la siguiente: la función lineal f(x)=x

Al pasar los dos resultados obtenidos tendríamos: f(6)=6 y f(11)=11 y tenemos la primer capa resuelta, pero aun falta la segunda capa en la cual haríamos el mismo proceso.

Hagamos:

En los nodos azules obtuvimos 6 y 11, 6 para el de arriba 11 para el de abajo. Nos colocamos en el nodo naranja de arriba y vemos qué datos y pesos están entrando así como el umbral.

estamos colocados aqui 👇 

y observamos que este nodo recibe 6 y 11 los resultados de los primeros nodos o capas y como pesos recibe 3 y 2, hacemos los cálculos v= (6)*(3) + (11)*(2) + 1=41 y para el segundo nodo el de abajo seria v= (11)*(1) + (6)*(5) + 1=42 estos resultados obtenidos los enviamos a la función de activación y tendríamos  f(41)=41y f(42)=42, hemos terminado.

Tarea resuelve los siguiente problemas.

Bueno esto lo hemos recordado pues es necesario conocer como funcionan las redes neuronales, el día miércoles estaré subiendo la segunda parte de la clase donde hablaremos más a fondo de una de las redes neuronales no supervisadas y supervisadas. Para pasar lista deja un comentario con tu nombre en la parte de abajo.👇 También si tienes dudas de como se resolvieron los problemas planteados, deja un comentario para que lo resolvamos.